FISICOM

Unidade 01: Cinemática
Aula 03 - Gráficos (MRU)
1. Posição por tempo (s x t):
Vamos ver agora uma outra forma de representar o movimento retilíneo uniforme: os gráficos.
Começaremos com exemplos para deixar mais fácil.
Vamos imaginar um carro movendo-se por uma estrada reta. Digamos que no início do movimento, isto é, quanto o tempo é igual a zero, sua posição também é zero. Então começa a contagem do tempo e o carro começa a assumir posições diferentes. Digamos que seus tempos e posições são dados pela tabela abaixo:
Com base nessas informações, vamos fazer o gráfico do movimento:
Note algumas coisas: como o carro partiu da origem (s = 0) no tempo inicial (t = 0), o primeiro ponto marcado é na origem do gráfico. A segunda posição que temos pela tabela é 80 km, ela acontece quando o tempo é igual a 1 h. Esse é o nosso segundo ponto.
Vamos continuando: o terceiro ponto representa a posição 160 km, quando o tempo é 2 h. O mesmo processo serve para colocar os outros pontos, observando as posições e tempos.
Observe que a reta é inclinada para cima. Isso significa que o móvel está andando para posições cada vez maiores. Logo, sua velocidade é positiva. Então temos que:
No gráfico posição por tempo (s x t), a reta representa a velocidade. Se ela está inclinada para cima, significa uma velocidade positiva.
Vamos para o próximo exemplo. Agora, digamos que nosso carro tem o movimento representado por essa outra tabela:
Qual sua posição inicial? Bom, no tempo igual a zero, sua posição é 360 km, logo, essa é sua posição inicial. Conforme o tempo passa, o carro ocupa posições cada vez menores. Vamos fazer seu gráfico para ver mais detalhes:
Colocando os valores da tabela no gráfico, podemos ver que a reta tem inclinação para baixo. Isso indica duas coisas: o carro move-se para posições cada vez menores e, sua velocidade é negativa. Então temos que:
No gráfico posição por tempo (s x t), a reta representa a velocidade. Se ela está inclinada para baixo, significa uma velocidade negativa.
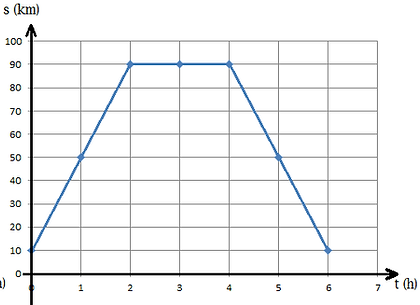
Observe agora outro gráfico:
Que tipo de informações podemos tirar dele? Bom, em primeiro lugar, podemos ver que sua posição inicial é 10km. Depois vemos que no tempo igual a 1h, ele ocupa a posição 50km. Isso quer dizer que ele alterou sua posição de 10 km para 50 km em 1 h. A segunda posição ocupada pelo carro é 90 km, o que acontece no tempo 2 h.
Perceba que, desde o início do movimento até o tempo de 2 h a reta possui inclinação para cima, logo a velocidade é positiva nesse trecho. Mas o que acontece entre 2 a 4 h?
O carro permaneceu na posição 90 km, isso quer dizer que ele não se moveu. Logo, a inclinação é zero, pois a velocidade também é zero. E após o tempo de 4 h?
Sua posição passa de 90 km para 50 km (t = 5 h) e depois passa de 50 km para 10 km (t = 6 h). Isso significa que o carro está ocupando posições cada vez menores. Como a inclinação da reta é para baixo, sua velocidade agora é negativa.
Aqui temos uma informação nova:
No gráfico posição por tempo (s x t), se a reta está na horizontal, a velocidade é nula.
Bom, se você entendeu, tente descrever o que está acontecendo no gráfico apresentado abaixo:
E ai? Conseguiu?
Já estamos acabando a análise gráfica. Agora só faltam alguns detalhes: como calcular a velocidade e o deslocamento através dos gráficos. Vamos ser bem objetivos aqui.
Para calcularmos a velocidade pelo gráfico (s x t), basta obtermos a inclinação da reta. Quanto mais inclinada, maior a velocidade, quanto menos inclinada, menor a velocidade. O sinal da velocidade já foi discutido lá em cima.
Vamos ver um exemplo: olhe novamente o gráfico do primeiro exemplo:
Para obtermos a velocidade, devemos obter o coeficiente angular da reta.
Em outras palavras, achar a inclinação da reta. Para isso, podemos pegar duas posições e seus respectivos tempos:
Vamos escolher:
s1 = 80, t1 = 1
s2 = 240, t2 = 3
Assim temos: v = ∆s = s2 - s1
∆t t2 - t1
Substituindo: v = 240 - 80 = 160 = 80 km/h
3 - 1 2
Caso quiséssemos encontrar a velocidade no segundo exemplo:
Vamos escolher duas posições e seus tempos:
s1 = 360, t1 = 0
s2 = 90, t2 = 3
Assim temos: v = ∆s = s2 - s1
∆t t2 - t1
Substituindo: v = 90 - 360 = -270 = -90 km/h
3 - 0 3
Observe o sinal negativo na velocidade.
Mas se desejássemos calcular quanto o carro andou, o seu deslocamento? Para isso, podemos usar um outro gráfico, o da velocidade pelo tempo (v x t).
2. Velocidade por tempo (v x t):
Como dissemos antes, podemos ter velocidade positiva, negativa ou nula. Como no MRU a velocidade é constante (por trechos), teremos gráficos que também são retas. Observe os três casos:
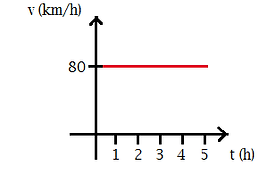
Velocidade positiva:
Usamos a velocidade do primeiro exemplo.
Perceba que conforme o tempo passa, a velocidade permanece
a mesma, 80 km/h. A reta está acima do eixo dos tempos.
Velocidade negativa:
Usamos a velocidade do segundo exemplo.
Perceba que conforme o tempo passa, a velocidade permanece
a mesma, - 90 km/h. A reta está abaixo do eixo dos tempos.
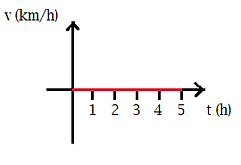
Velocidade nula:
Em caso de velocidade nula, temos um gráfico onde a reta que
representa a velocidade ficaria em cima do eixo dos tempos.
Usando gráficos (v x t), podemos calcular o deslocamento.
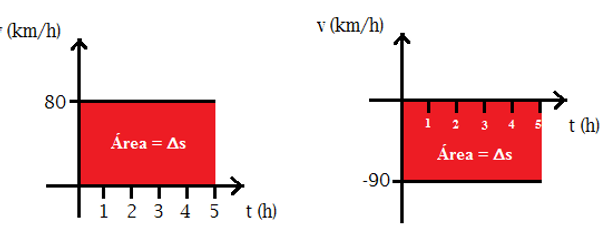
Para isso basta calcularmos a área que se forma entre a reta da velocidade e o eixo dos tempos:
Veja os exemplos:
No primeiro caso temos um retângulo, cuja base vale 5 e altura 80. Assim, a área vale:
A = base x altura = (5 h) x (80 km/h) = 400 km
No segundo caso temos um retângulo, cuja base vale 5 e altura 90. Assim, a área vale:
A = base x altura = (5 h) x (-90 km/h) = - 450 km *
* Aqui há um detalhe: como a velocidade é negativa, temos um deslocamento negativo. Apesar de não existir área negativa, esse sinal indica apenas que houve um deslocamento negativo, isso é, a posição final ocupada pelo carro é menor que a posição inicial (entenda como: posição final está à esquerda da posição inicial).
Vamos discutir algumas situações:
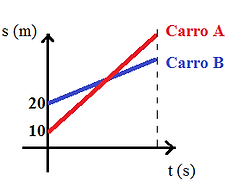
Imagine que numa prova você esteja analisando o gráfico ao lado:
Então o professor questiona: qual carro possui a maior velocidade?
Observe as inclinações das retas. Qual delas possui maior inclinação?
Obviamente é a relativa ao carro A. Logo, ele terá a maior velocidade.
Mas se você ainda não se convenceu, então observe outras informações.
Temos as posições iniciais, correto, mas não foram dadas as finais. Entretanto, basta olhar o gráfico para ver que o carro A, no mesmo intervalo de tempo, vai ocupar uma posição final maior que o carro B, pois o final de sua reta atingiu ponto mais alto que o final da reta relativa ao carro B. Então pensemos: se o carro A saiu da posição 10 e atingiu uma posição maior que o B, e o carro B saiu da posição 20 e atingiu uma posição menor que o A, qual deles teve o maior deslocamento num mesmo intervalo de tempo? Lembrando que deslocamento é a diferença entre as posições final e inicial.
Certamente, no mesmo intervalo de tempo, quem teve maior deslocamento foi o carro A, como velocidade média é deslocamento dividido por tempo, o carro A terá maior velocidade.
Agora observe outra situação:
No gráfico ao lado destacamos um ponto especial. Quando estamos
analisando gráficos s x t, e quando há mais de uma reta no mesmo
gráfico, como é o caso, o ponto onde uma reta cruza a outra é o local
onde os carros (nesse caso) se encontram.
Observe que, no instante te (te = tempo de encontro) os carros ocupam
a mesma posição se (se = posição de encontro).
Assim, se as retas se cruzarem significa que os carros se encontraram
naquele ponto. Isso, por exemplo, pode significar uma ultrapassagem, ou apenas cada carro indo para seu lado, como é o que aconteceu no gráfico ao lado. Enquanto o carro A movimentava-se para a direita, o carro B movimentava-se para esquerda. Num certo momento, eles se cruzaram.
No primeiro exemplo, onde as duas retas possuíam inclinação para cima, o carro A ultrapassou o B, pois apesar do carro A sair de uma posição menor, possuía maior velocidade.